km-trends
| Edit this page | Report an issue |
線形代数2022
設問1(LU分解)
LU分解の利点
- 2つの行列L,Uを格納するのに必要なメモリは、元の行列Aの格納スペースに等しい1。
- Ax=bの方程式を解くとき、1度LU分解をすればbの値が変化してもすぐに解ける2。Gaussの消去法を使う場合、拡大係数行列を再度階段化し直す必要がある
5つの行列分解
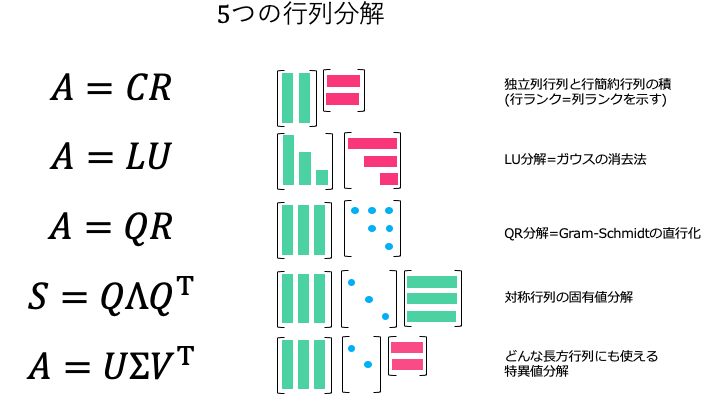
CR分解
$A$ の独立な列行列のみからなる行列 $C$ と、行簡約行列 $R$ の積に分解する。
行ランクと列ランクが等しいことの証明に使える。
例:
一般に $A:m\times n,\ C:m\times c,\ R:c\times n$ とするとき、$A$ の列ランクは $C$ の列数 $c$ である。また、$R$ の行ベクトルは $R$ が行簡約が独立であることより、$A$ の行ランクは、
LU分解
QR分解
固有値分解
特異値分解
プログラム
解答の確認に使ったプログラム
- ans_check.py
- LU_original.py
- LU_scipy.py:科学計算ライブラリを使ったLU分解。浮動小数点で計算するため結果にズレが生じる?
設問2(四元数の正方行列表現)
四元数はコンピュータビジョンと関係がある3。出題者が西野教授…?